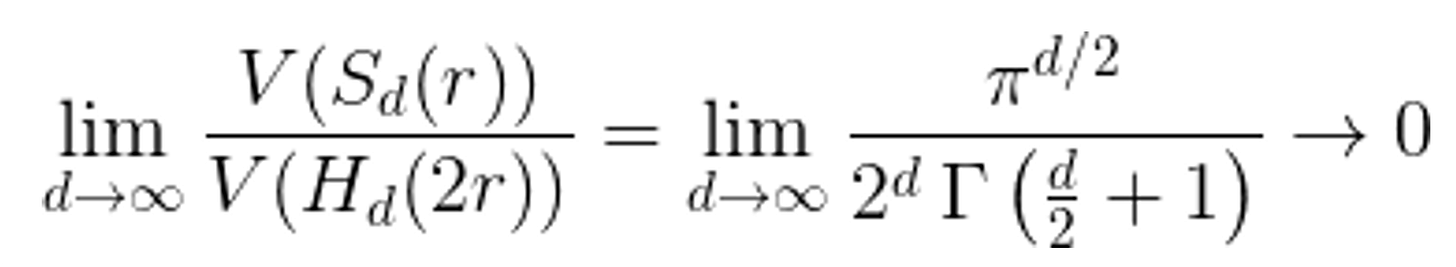Interpolation, Extrapolation, Integration - On Data and Models in Bio

What to make of what we learn in bio and beyond

Two of the biggest outstanding questions in AI applied to biological contexts are:

1. Will we be able to learn new information? E.g., hallucinating a cure for cancer?

2. How to best integrate disparate data sets

These questions are different in their tactical applications, but both fundamentally deal with the representation spaces of data — what exists, what doesn’t exist, and what is a real approximation of reality.

There are often very strong opinions voiced on the mechanistic side of deep learning that sound sensible enough. These perspectives are explicitly reductionist — along the lines of “it’s all just matrix multiplication” and take the position that it is epistemologically impossible for a model to produce new knowledge beyond the scope of the data it has been trained on. On the other hand, AI-enthusiasts particularly in bio, often champion the idea that "hallucinations" may be features as opposed to bugs and represent potentially new knowledge. Prominent researchers muse that we will be able to use deep neural networks to reason our way toward a cure for cancer or that hallucinated proteins produced by diffusion or autoregressive models may indeed have novel and beneficial properties. Generally, those on the biological side have downplayed this as hype, sometimes with good reason -- or often no reason.

A good portion of this question revolves around the idea of extrapolation and interpolation — e.g., what information is contained within the data set. This is a red herring argument for the most part, as this article will outline.

A second dimension of this question which be touched on briefly toward the end of this article, and has been discussed in more detail in an article on “AI Mathematicians and Scientists”¹, is how generative models can be combined with reinforcement learning to enable reasoning. This approach is potentially very powerful if there are good evaluation functions for reinforcement, however, may be somewhat less applicable if such explicit functions are not well defined as may be the case in many biological applications.

This article aims to describe what is mathematically meant by interpolation and extrapolation in high dimensional spaces for a semi-technical audience and what it might mean especially in the context of multimodal data for the generation of "new knowledge". A second aim is to describe why the concept of "new knowledge" is itself not very well defined in the life sciences and why a major driver of this relates to issues encountered in biological variability, data manipulations required for dataset integrations, and the validity of hallucinated data in the context of functional degeneracy -- or the physical reality of lower dimensional permitted states of physical systems.

In the end, we may conclude that the idea of "new knowledge" generation by deep neural networks will simply follow the maxim "There is nothing new under the sun". Discovery is a matter of either being exposed to new information (training data) or finding new remixes. A tiny bit of the former leads to an exponentially increasing scope of the latter.

Interpolation and Extrapolation -- A Basic Primer

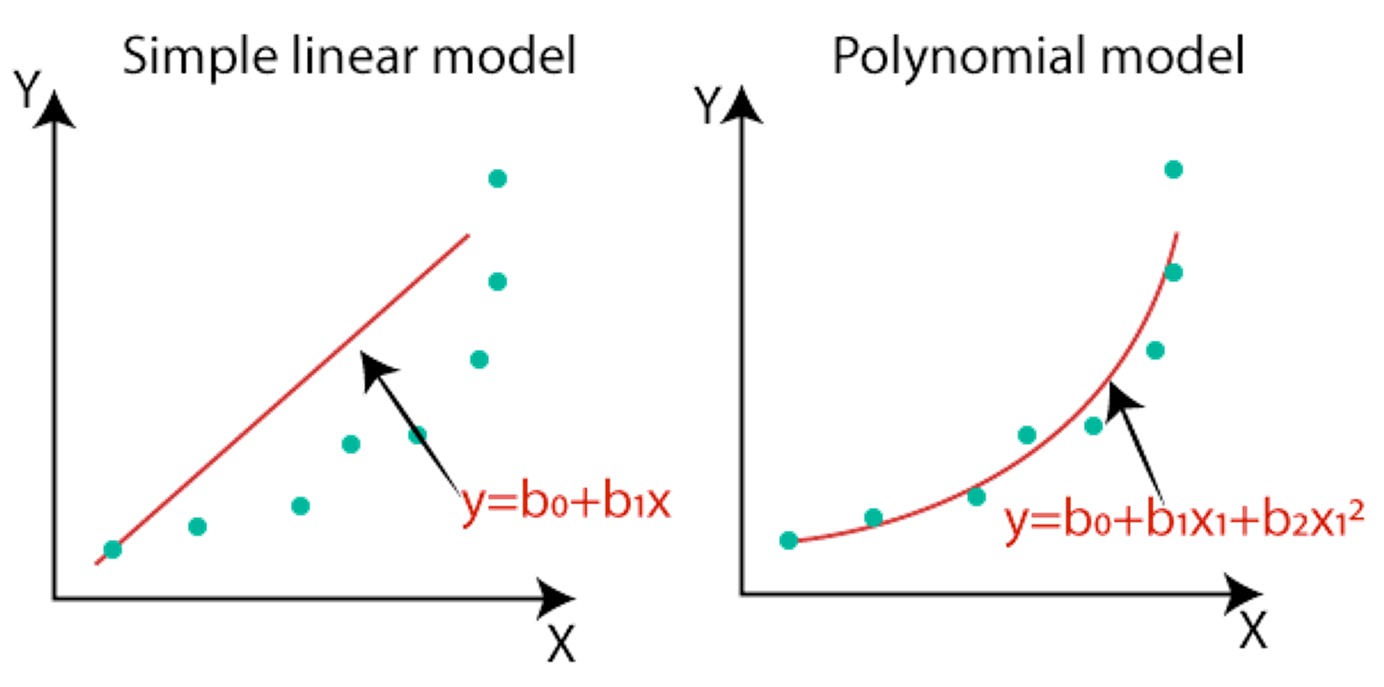
Neural networks are often considered universal function approximators. They take a large number of data points and attempt to create a function that threads a needle through all of them with high fidelity. The simplest version of this is a linear regression, but there are other models like polynomial approximations, splines, etc. If one were to write out the actual algebraic function of a deep neural network it would be massive (think billions of terms all added together) and would largely be composed of linear combinations with a host of non-linear checkpoints like ReLUs, normalizations, etc. The goal, however, is to essentially thread a needle (or plane or hyperplane) through a large number of data points.

Figure 1: Basic function approximators. This is a 2D case while deep neural networks work in hundreds or thousands of dimensions².

When speaking about "interpolation", the concept is that you should be able to take a hypothetical point between your existing data points and use a neural network to accurately predict the value of that point. Part of the effort of training a deep neural network is to try and create a smooth and continuous function between data points -- depending on how close the data points are in space, this may or may not be reflective of reality, but interpolation presumes that it is. The collective space that is enclosed by such a curve fitting over a data distribution is referred to as the "convex hull". It is convex because it takes a closed shape such that any two points inside the shape can be connected by a line that does not leave the shape -- anything therefore within this shape is considered an "interpolated space". It's important to make a distinction between this domain of interpolation and the actual validity of the function approximation in that space. These are two separate things -- one relates to the scope of the data distribution and the other to how good the model is within that range.

Figure: A basic example of a convex hull that bounds a set of data points. It contains all of the data points and is convex such that any two interior points can be connected linearly within the shape providing a path for continuous interpolation³

The question of extrapolation then basically amounts to what a model (or a function) says about a point that is outside of this convex hull. From a naive perspective, there is no particular reason to believe that a function is (or isn't) extensible beyond a certain domain. For example, if data mirroring a sine wave were modeled on a small part of the x-axis, it would be infinitely generalizable. However, if the same data were part of a packet signal, it would not.

Figure: The ability to extrapolate a curve beyond a training set depends on assumptions of its consistency. The left image is simple, but if one were to sample only the middle of the right image, it would not likely extrapolate well outside of the training set⁴

The Extrapolation/Interpolation Question is Moot

The interpolation/extrapolation question is a red herring, mathematically speaking -- it's pretty much guaranteed that in any high dimensional space, any randomly selected data point will be outside of the convex hull of any training data. This was assessed comprehensively in a 2021 article from FAIR titled "Learning in High Dimensions Always Amounts to Extrapolations"

Ref⁵

While the shape of a convex hull of any data distribution is unique (and difficult to visualize), a more intuitive approach can be seen by the trends of circles in squares or spheres in cubes. The trend is that as the dimensionality increases, the % of the overall volume that is occupied by a hypersphere that is increasing its primary dimension in parallel to a hypercube goes to zero. This is the "curse of dimensionality".

Figure: V(S) is the equation for the volume of a hypersphere and V(H) is for a hypercube. The ratio goes to zero as the dimension increases meaning that any convex space in a high dimensional space occupies ~0% of the total volume. Almost every point is an extrapolation of the original data set⁶

The conclusion from the paper is that:

...The above result effectively demonstrates that when sampling uniformly from a hyper ball, the probability that all the points are in a convex position (any sample lies outside of the other samples’ convex hull) is 1 when the number of samples grows linearly with the dimension, even when adding an arbitrary constant number of samples, M.

Consequently, it is almost certain that any uniformly selected point passed through a high-dimensional model will not be within any interpolation domain of the model. Everything is likely considered an extrapolation.

But this may not be too problematic -- at least for biological systems.

Inherent Biological Structure Likely Enables Broader Extrapolation

While there is structure in all data, some are more constrained than others. In general, systems-level data, like biology, while being very high dimensional, have significant constraints -- either reflected in factors like homeostasis or transition paths such as cell differentiation or other programmatic processes. Diseases typically result from-or-in off-distribution states and may be less constrained such as high mutational phenotype cancers. Using neural networks as function approximators to learn these constraints is known as manifold learning which learns to represent complex system states in a lower-dimensional format. An example of manifold learning is described in Norman et. al⁷ as it relates to the genetic perturbation landscape of transcriptomic single-cell states.

Figure: Cell states that might have very high dimensional data sets generally exist on a much lower dimensional surface or manifold that is constrained by states compatible with gene regulation or survival. These constraints may enable a broader range of extrapolation than might exist in an unconstrained system because the dimension of the actual system is lower (Norman et. al.)

Manifold learning itself does not necessarily ensure more effective extrapolation, however, it does potentially simplify the problem and, combined with prior knowledge about cell states, for example, that are not compatible with life, may provide a broader set of boundary conditions to extend a neural network's predictive capability beyond the scope of any specific training set.

One key point to be aware of in dimension reduction is that visual representation in reduced spaces such as UMAP plots can skew the interpolation/extrapolation domains of the original data and create the visual appearance of interpolation where it does not exist. The paper from FAIR noted this effect:

We observe that dimensionality reduction methods lose the interpolation/extrapolation information and lead to visual misconceptions significantly skewed toward interpolation

Reduced dimensionality manifold learning may be quite powerful in contexts where there is substantial degeneracy. This is one of the reasons why protein modeling has been so successful. The space of possible structures for an amino acid sequence is extraordinary, however, some inherent practical constraints reduce the dimension. For example, proteins that have evolved in the real world have specific functions -- and structures that support those functions. While this space remains large, the space of proteins that likely have a biological function is a subset of the space of possible configurations.

This is not the same, for example, with small molecules that do not expressly need to have any biological function in a training set. The concept of degeneracy has been described in more detail in a recent post by Michael Bronstein on the role of data generation in training deep learning models⁸.

Data Processing and Integration Can Be Confounders

If we move beyond the artificial constraints of interpolation and extrapolation and appreciate that neural networks can benefit from the existence of a lower dimensional manifold even in a high dimensional data space, we still have to confront the issue of what information the data space contains and whether it is a good approximation of reality. In biology, this is particularly acute because data that is generated from physical processes has a wide range of potential confounders and, to reach a sufficient data set scale, must be combined from multiple experiments, whether done in a single pipeline or integrated across many.

Life science research, as a category, has largely been a discipline characterized by labels and ontologies. Cells have been described by names, such as A549 or glial cells, not explicitly by their composition. This is useful at a descriptive level but is much less so from an analytical level, especially for machine learning applications where technical variation and compositional distributions are highly impactful for training a model. This issue has implications on both sides of a model -- on the upstream side of data generation, variability might be introduced across both technical and biological dimensions and may consist of factors as small as specific reagents that are used, timing of the cell cycle, distribution of sequences in library preps, genetic composition difference, capture efficiencies for sequencing, etc. All of these factors influence the raw data being collected. On the analysis end, these same measurements are used for clustering and classification to identify and label cells.

Many tool sets have been developed to process biological datasets (specifically single-cell datasets). A recent preprint analyzed the impact of some protocols on downstream data interpretation.

Ref⁹

In short, this paper wanted to assess the impact of different computational processing steps on the representations of single-cell data sets to understand how much the algorithms may alter the underlying data. To do so, they took a single set of data and divided it into pseudo batches, processed each batch separately, reintegrated each set, and compared pre and post-processing results. The basic conclusion from the authors is below:

In particular, MNN, SCVI, and LIGER performed poorly in our tests, often altering the data considerably. Batch correction with Combat, BBKNN, and Seurat introduced artifacts that could be detected in our setup. However, we found that Harmony was the only method that consistently performed well, in all the testing methodologies we present. Due to these results, Harmony is the only method we can safely recommend using when performing batch correction of scRNA-seq data.

To visualize, they use a metric they called k-NN (nearest neighbor) rank displacement

Figure: see description (from previous ref)

and determined that each algorithm respectively had the following impact on the would-be data composition if used for multi-batch integration

Figure: the average rank displacement from using different batch integration processing methods on the same data set with randomly processed pseudo batches shows how processing affects the underlying data (from previous ref)

An interesting observation here is that simpler approaches for batch correction such as PCA and Seurat retain more of the original data representation than more complex deep learning models like scVI.

This is particularly relevant if integrated data sets are going to be used as training data for deep learning models, and if a requirement for doing so is that they are first integrated into a common representation format. The analysis above indicates that most batch integration methods can substantially affect the representational context of individual data points, but it is not directly apparent how or whether the changes are meaningful as they relate to training downstream models.

So what about new knowledge?

The concept of new knowledge has a few different contexts. The first is one of the discovery of information already contained within data. On this point, deep learning models will certainly be able to elucidate new information, but this is more akin to bringing already existing information to light. The identification of a specific cluster of Norn cells in the recent Universal Cell Embedding model¹⁰ is an example of this. This will only increase with increasingly multimodal data sets.

Will these models extrapolate? Yes, certainly, however, we should consider that while biology is a continuum, we have limited sample data points, and often our ability to measure transition states is less precise. Combining dynamical time models with joint embedding models may provide a more mechanistic form of extrapolation.

Will generative modeling produce novel biology/chemistry? I expect so, for example, some of the recent work from the Baker lab¹¹ has indicated that antibodies have been created that do not contain homology to existing known antibodies.

Does this mean that AI can be creative? I think the answer to this is yes, and creativity expands with multimodality. The argument that AI cannot extrapolate beyond its training set or create new knowledge is a misinterpretation of what knowledge is and a somewhat hubristic viewpoint that humans can identify the information content within a data set. However, the same framework could equally as well be applied to humans. We each have our training sets -- and they are the collection of experiences that we have during our lives. They are multimodal for sure, but when we dream up new creative endeavors, we are not necessarily producing ideas that are completely foreign to anything we have ever seen or experienced, we are combining, recombining, approximating, abstracting, and synthesizing — all things that neural networks are capable of.

Architectures for New Knowledge

This article has largely focused on the scope of generative models and the ideas of whether such models are valid outside of their training domain. However, newer architectures that combine generation with search/reinforcement can also be powerful knowledge generators. A requirement of this approach is a good evaluation function for reinforcement — most of these to date have been mathematical. This was discussed previously in “AI Mathematicians and Scientists” and is also the subject of the more recent publication of FunSearch¹² by Deepmind which introduced a model for code generation that could be used to find novel algorithms and an evolutionary recombination of generated code for reinforcement learning. In this case, an explicit evaluation function for code performance was used to rank order generated outputs. Combining generation, recombination, and evaluation is akin to automating a thinking process and is a powerful paradigm to produce new insights.

I expect that AI models will continue to increase in their abilities with increasing data in the case of generation, and architecture development in the case of reinforcement learning. What is contingent on model builders is that the data and evaluation functions are accurate reflections of the real world.

Extrapolation is an inevitability and I expect that we will be surprised with what can be discovered in the datasets of our world that we, as humans, may not even be aware of.

References

1.

2. https://medium.com/analytics-vidhya/understanding-polynomial-regression-5ac25b970e18

3. https://en.wiktionary.org/wiki/convex_hull

4. https://demonstrations.wolfram.com/SineGaussianSignals/ & https://alearningaday.blog/2017/04/10/life-sine-wave/

5. https://arxiv.org/abs/2110.09485

6. https://tex.stackexchange.com/questions/207772/hypersphere-inscribed-within-hypercube

7. https://www.science.org/doi/10.1126/science.aax4438?url_ver=Z39.88-2003&rfr_id=ori:rid:crossref.org&rfr_dat=cr_pub%20%200pubmed

8. https://towardsdatascience.com/the-road-to-biology-2-0-will-pass-through-black-box-data-bbd00fabf959

9. https://www.biorxiv.org/content/10.1101/2024.03.19.585562v1.full

10. https://www.biorxiv.org/content/10.1101/2023.11.28.568918v1

11. https://www.biorxiv.org/content/10.1101/2024.03.14.585103v1

12. https://deepmind.google/discover/blog/funsearch-making-new-discoveries-in-mathematical-sciences-using-large-language-models/